Wartość Shapleya w modelowaniu atrybucji

Modele atrybucji data-driven analizują ścieżki konwersji i na tej podstawie próbują określić wkład poszczególnych interakcji w doprowadzenie do konwersji, niejako zwalniając nas z konieczności podejmowania arbitralnych decyzji w tym zakresie. Wartość Shapleya jest funkcją często wykorzystywaną przez algorytmy atrybucji opartej na danych, dlatego warto poznać ją bliżej.

Czym jest Wartość Shapleya?

Wartość Shapleya jest pojęciem z teorii gier, stworzonym w 1953 r. przez amerykańskiego matematyka Lloyda Shapleya. Określa sposób podziału zysku pomiędzy uczestników gry kooperatywnej, czyli takiej, w której gracze mogą łączyć się w koalicje celem uzyskania określonego wyniku.

Wartość Shapleya określa, jakiego zysku z całości powinien spodziewać się dany gracz, biorąc pod uwagę jego średni wkład w dowolnej koalicji.

Jeśli potraktować marketing jako grę, w której uczestniczą różne kanały marketingowe, łącznie wypracowując wynik w postaci konwersji, to wartość Shapleya mogłaby posłużyć do przypisania wartości tym kanałom. Tym bardziej, że wartość Shapleya ma pewne właściwości, które dobrze wpasowują się w koncepcję modelowania atrybucji.

1 Suma wartości Shapleya dla wszystkich graczy musi być równa łącznemu wynikowi

Z punktu widzenia modelowania atrybucji jest to podstawowy warunek: konwersje przypisane poszczególnym kanałom muszą sumować się do łącznej liczby wszystkich odnotowanych konwersji.

2 Symetria

Gracze, którzy z punktu widzenia wyniku grają dokładnie taką samą rolę w grze, będą mieli identyczne wartości Shapleya. Jest to intuicyjny wymóg sprawiedliwego podziału wyniku i prawidłowego modelowania atrybucji.

3 Zerowa wartość gracza nieistotnego

Gracz, który nie wnosi nic do żadnej koalicji, będzie miał zerową wartość Shapleya. Innymi słowy, bezwartościowym kanałom, które nie wpływają na wzrost konwersji, nie przypiszemy żadnej wartości.

4 Addytywność

Niezależnie od tego, jak zdefiniujemy wynik danej gry, czy będzie to wynik A, wynik B, czy suma wyników A + B, to dla każdego gracza i:

Shi (wynik A) + Shi (wynik B) = Shi (wynik A + wynik B)

Aby łatwiej było zrozumieć tę ostatnią właściwość wartości Shapleya, zilustruję ją na przykładzie. Załóżmy, że mamy klika rodzajów konwersji: transakcja, subskrypcja newslettera i pobranie e-booka. Addytywność oznacza, że suma wartości Shapleya dla poszczególnych rodzajów konwersji będzie wartością Shapleya dla konwersji liczonych łącznie. Jeśli więc: konwersje = transakcje + pobrania pliku + subskrypcje to dla każdego kanału i:

Shi (konwersje) = Shi (transakcje) + Shi (pobrania pliku) + Shi (subskrypcje)

Przy segmentacji na poszczególne rodzaje konwersji jest to warunek konieczny, by wartość transakcji, subskrypcji i pobrań pliku przypisanych do danego kanału sumowała się do łącznej wartości konwersji przypisanych temu kanałowi.

Lloyd Shapley wykazał, że jest tylko jedna funkcja spełniająca te warunki i podał sposób na jej obliczenie.

Wkład marginalny

Aby zrozumieć formułę wartości Shapleya, musimy zaznajomić się z pojęciem wkładu marginalnego. Gracz w grze koalicyjnej może wchodzić w różne kombinacje graczy (różne koalicje). Mogą one mieć różny rozmiar (liczebność).

Najprostsza kombinacja to taka, w której bierze udział tylko dany gracz (rozmiar 1). Następnie może on utworzyć „dwuosobowe” kombinacje z każdym z innych graczy (rozmiar 2). I tak dalej, aż do kombinacji, w której biorą udział wszyscy gracze (rozmiar n, gdzie n to łączna liczba graczy). Kombinacje będą więc występować w n różnych rozmiarach, od 1 do n.

Korzyść z przyjęcia do danej koalicji określonego gracza (wzrost wyniku gry) może być różna dla każdej z tych kombinacji. Wkład marginalny gracza do danej kombinacji graczy określa, ile koalicja zyska na wyniku, jeśli dołączy do niej dany gracz. Obliczamy to w sposób następujący:

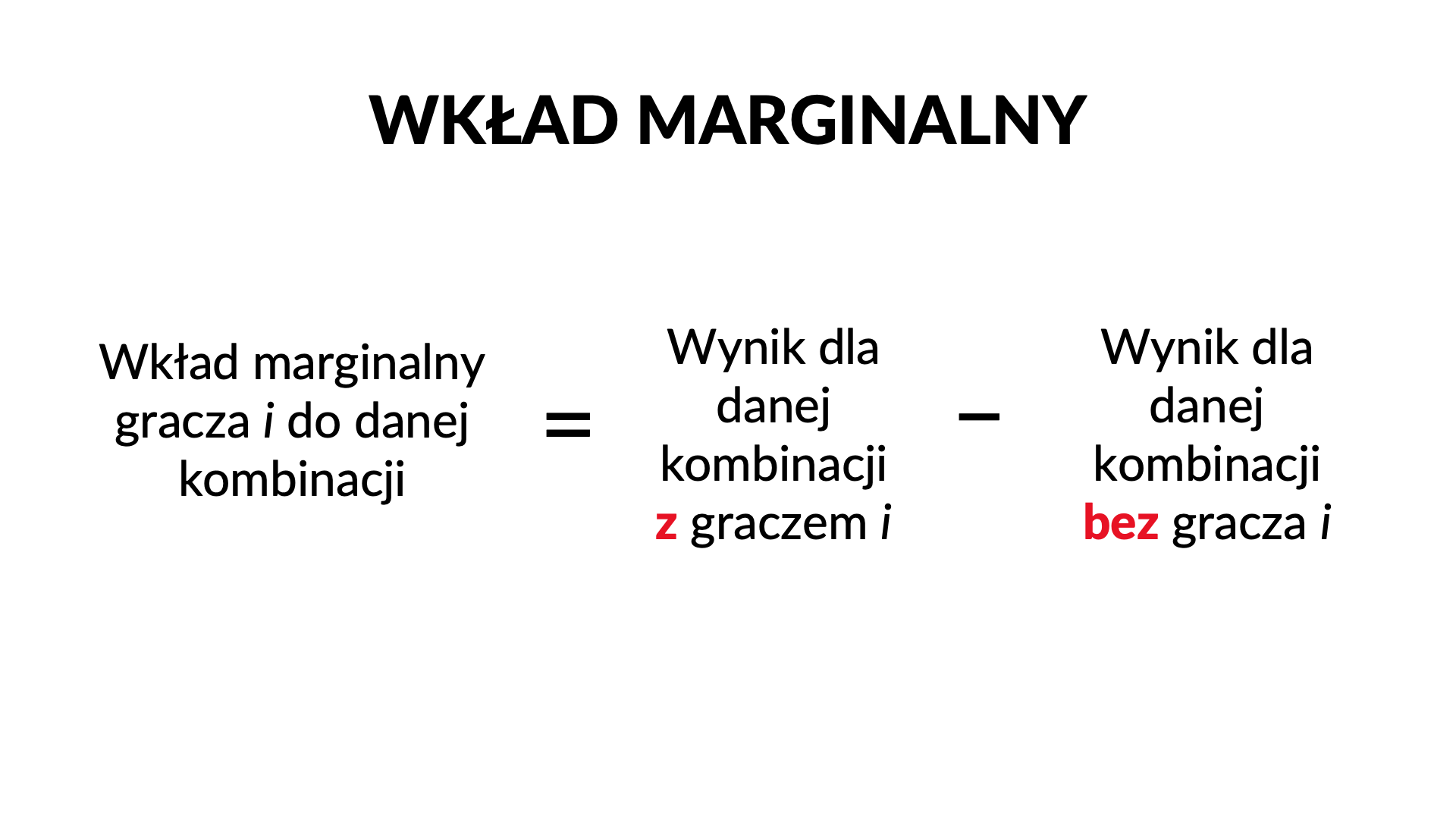
Koncepcję tę łatwo zrozumieć na przykładzie gry w przedsiębiorstwo, w skład którego wchodzą biznesmen B oraz pracownicy: P1, P2, P3. Każdy z pracowników jest w stanie wytworzyć przychód w wysokości jednej sakiewki. Firma, w której biznesmen zatrudnia trzy osoby, zarabia trzy sakiewki:

Jeśli pracowników będzie dwóch, firma zarobi tylko dwie sakiewki. Nie ma tu znaczenia, czy będą pracowali P1 z P2, czy P2 z P3, czy też P1 z P3 – dowolnych dwóch pracowników zatrudnionych przez biznesmena zawsze zarobi dwie sakiewki. Jeśli pracownik będzie tylko jeden, firma zarobi tylko jedną sakiewkę. Sam biznesmen bez pracowników nie zarobi nic. Bez biznesmena sami pracownicy też nie będą w stanie nic zarobić, niezależnie od tego, ilu ich będzie.

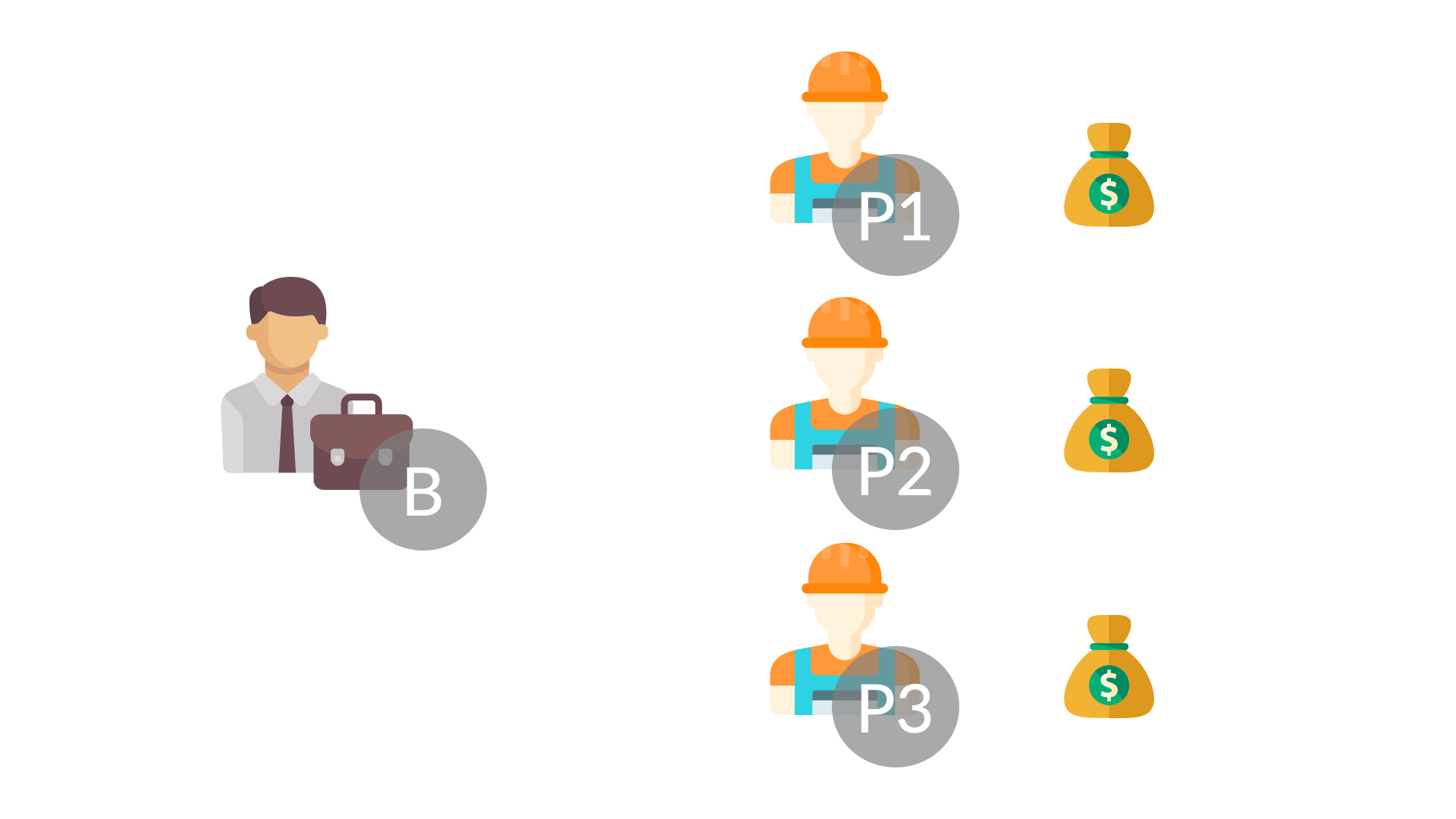
Zobaczmy teraz, jak liczyć wkłady marginalne – na przykładzie gracza P1. Kombinacja B, P2, P3 (biznesmen zatrudniający dwóch pozostałych pracowników bez P1) wytwarza dwie sakiewki:

A że firma w składzie (B, P1, P2, P3) zarabia trzy sakiewki, to wkład marginalny gracza P1 do koalicji B, P1, P2, P3 wynosi jedną sakiewkę (3 – 2 = 1).

Jak obliczać wartość Shapleya?

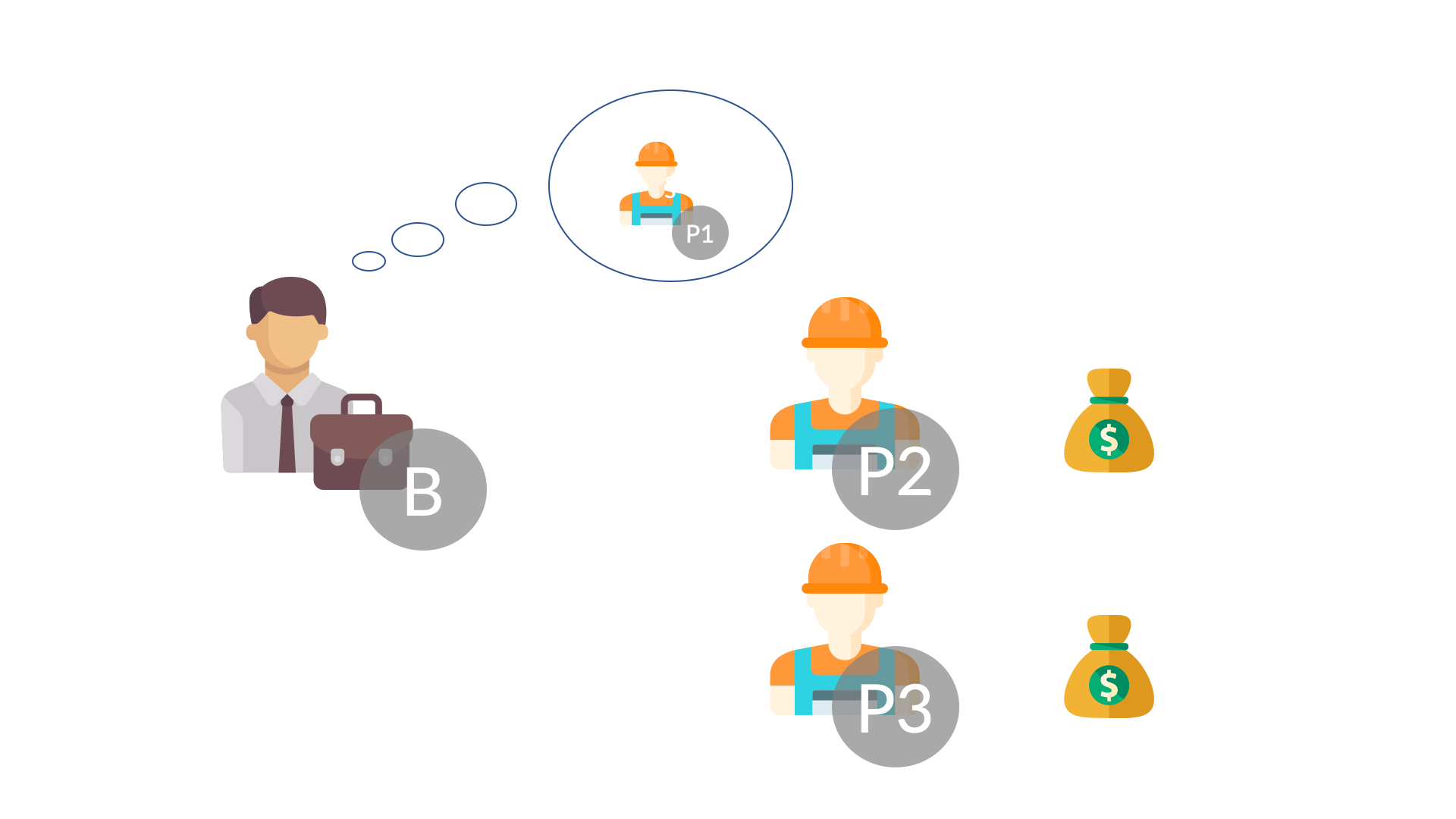
Formuła przypisania wartości danemu graczowi, odkryta przez Lloyda Shapleya, ma następującą postać:

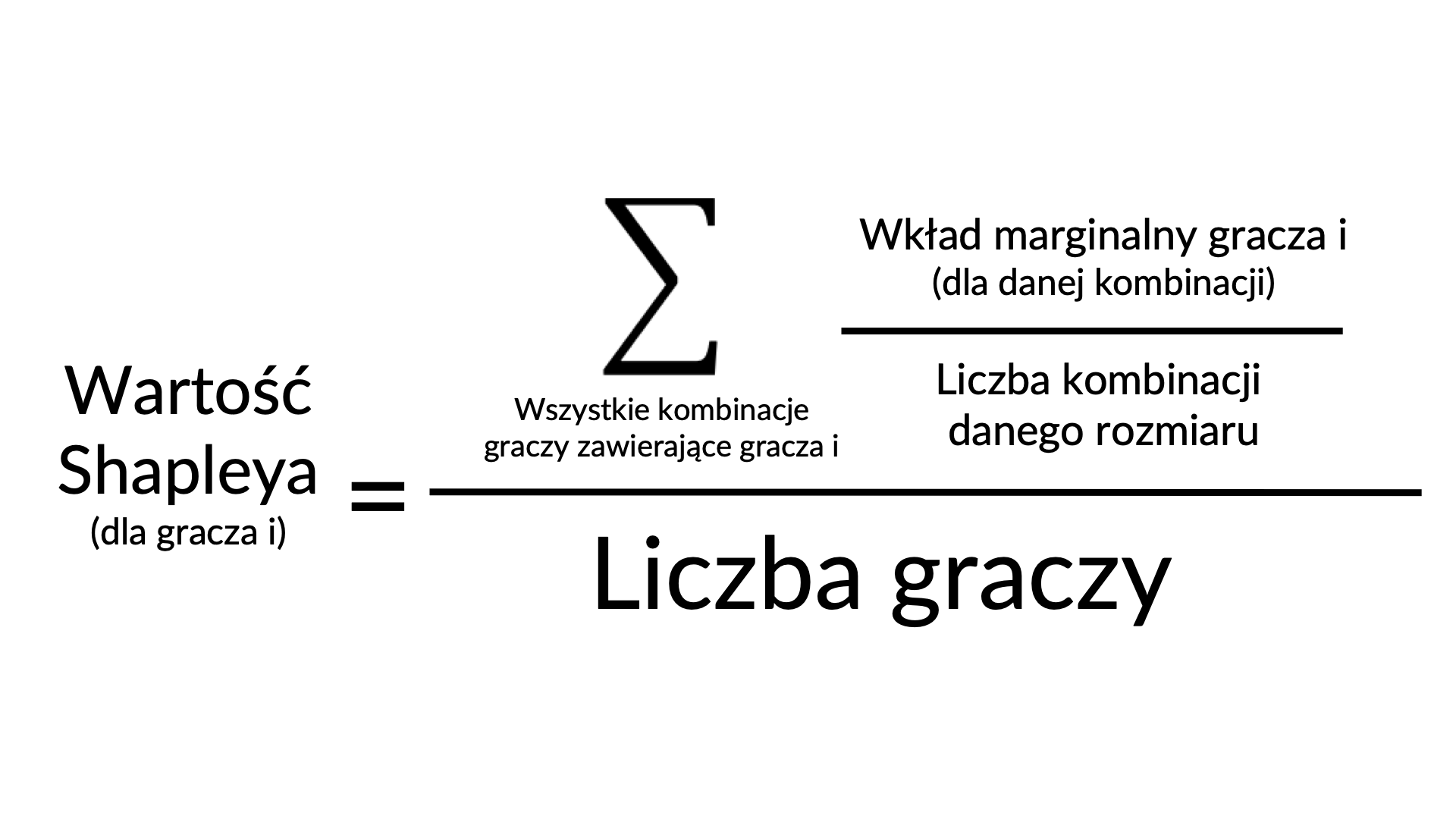
Wróćmy do naszego przykładu i zobaczmy, jak będą wyglądać wkłady marginalne gracza P1 do każdej z możliwych kombinacji z jego udziałem. Następnie dokonajmy obliczeń zgodnie z definicją wartości Shapleya:

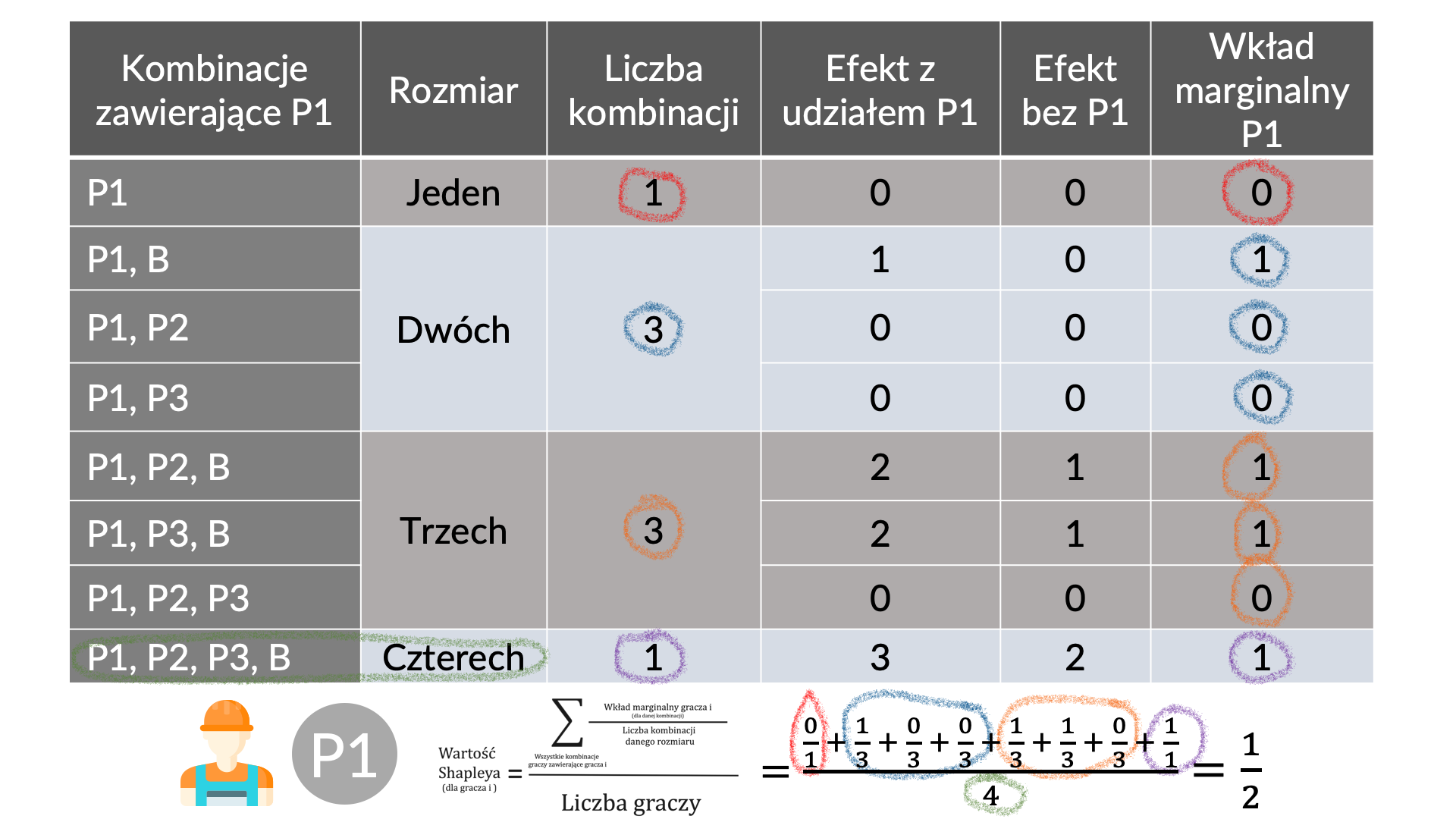
Wartość Shapleya dla gracza P1 wynosi Sh(P1) = 1/2 = 0,5. Podobne obliczenia należałoby wykonać dla pozostałych graczy, ale możemy też wykorzystać właściwości wartości Shapleya i dokonać obliczeń na skróty. Ponieważ rola graczy P1, P2 i P3 jest identyczna, wartość Shapleya dla tych graczy również będzie taka sama, czyli Sh(P2) = 0,5 oraz Sh(P3) = 0,5.

Wartości Shapleya dla poszczególnych graczy powinny sumować się do wyniku uzyskanego przez wszystkich graczy łącznie. Firma w pełnej obsadzie (P1, P2, P3, B) wytwarza trzy sakiewki. Biznesmen powinien otrzymać więc to, co zostanie z łącznego wyniku po „wypłaceniu” wartości Shapleya pracownikom:

Sh(B) = 3 – Sh(P1) – Sh(P2) – Sh(P3) = 3 – 0,5 – 0,5 – 0,5 = 1,5

Ogólnie rzecz ujmując, w grze biznesmen – pracownicy, wartość Shapleya dzieli wypracowany zysk w ten sposób, że połowa zysku przypada na biznesmena, drugą połowę dzielą między sobą pracownicy po równo (jeśli rola każdego pracownika jest taka sama).

Wartość Shapleya dla współczynnika konwersji

Zobaczmy teraz, jak obliczyć wartość Shapleya dla gry, w której różne kanały marketingu wypracowują wspólny wynik, którym jest współczynnik konwersji.

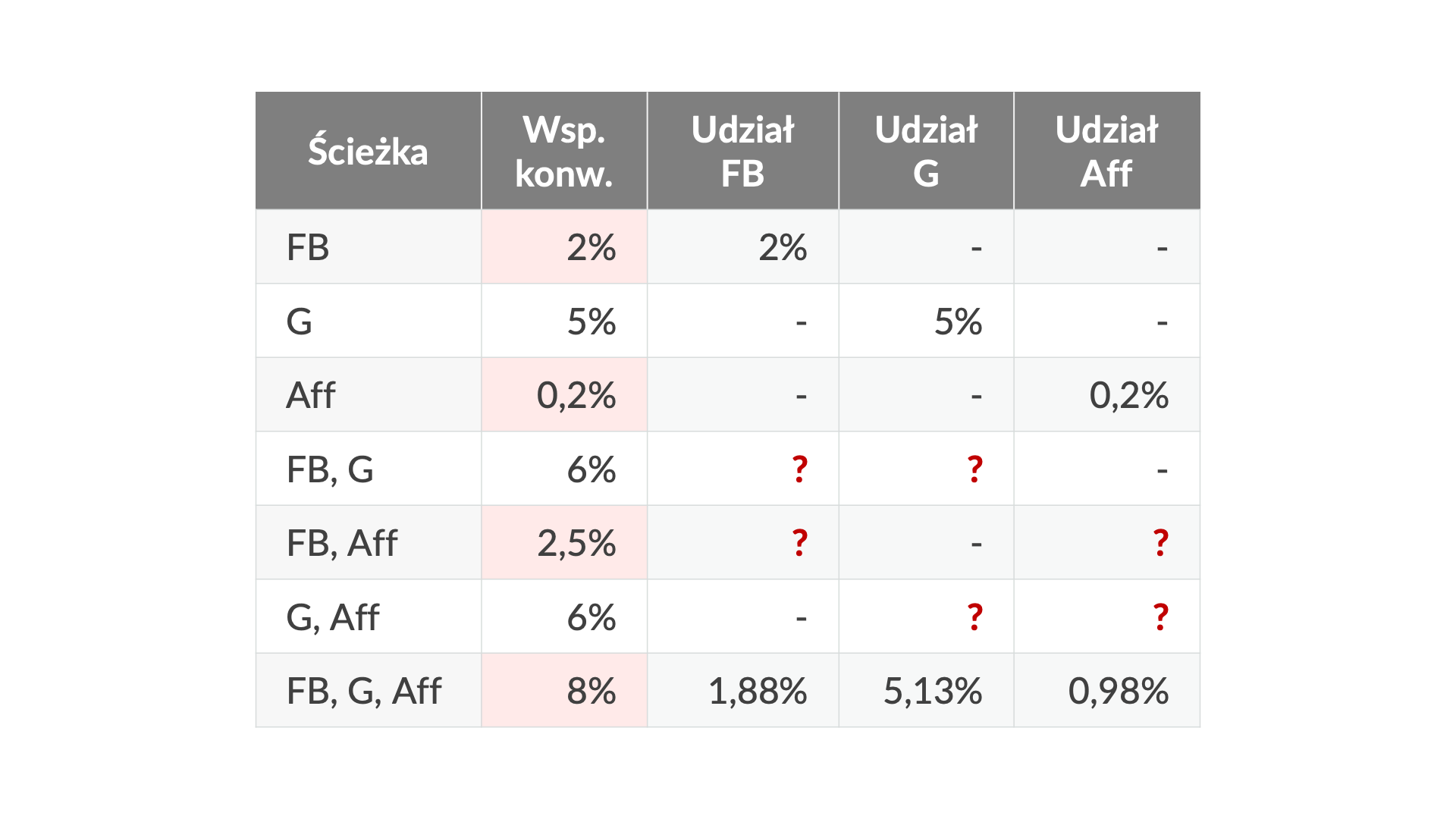
W naszym przykładzie będą występować trzy kanały: Google, Facebook i afiliacja. Oto liczby kliknięć i konwersji na ścieżkach zawierających wszystkie możliwe kombinacje tych kanałów:

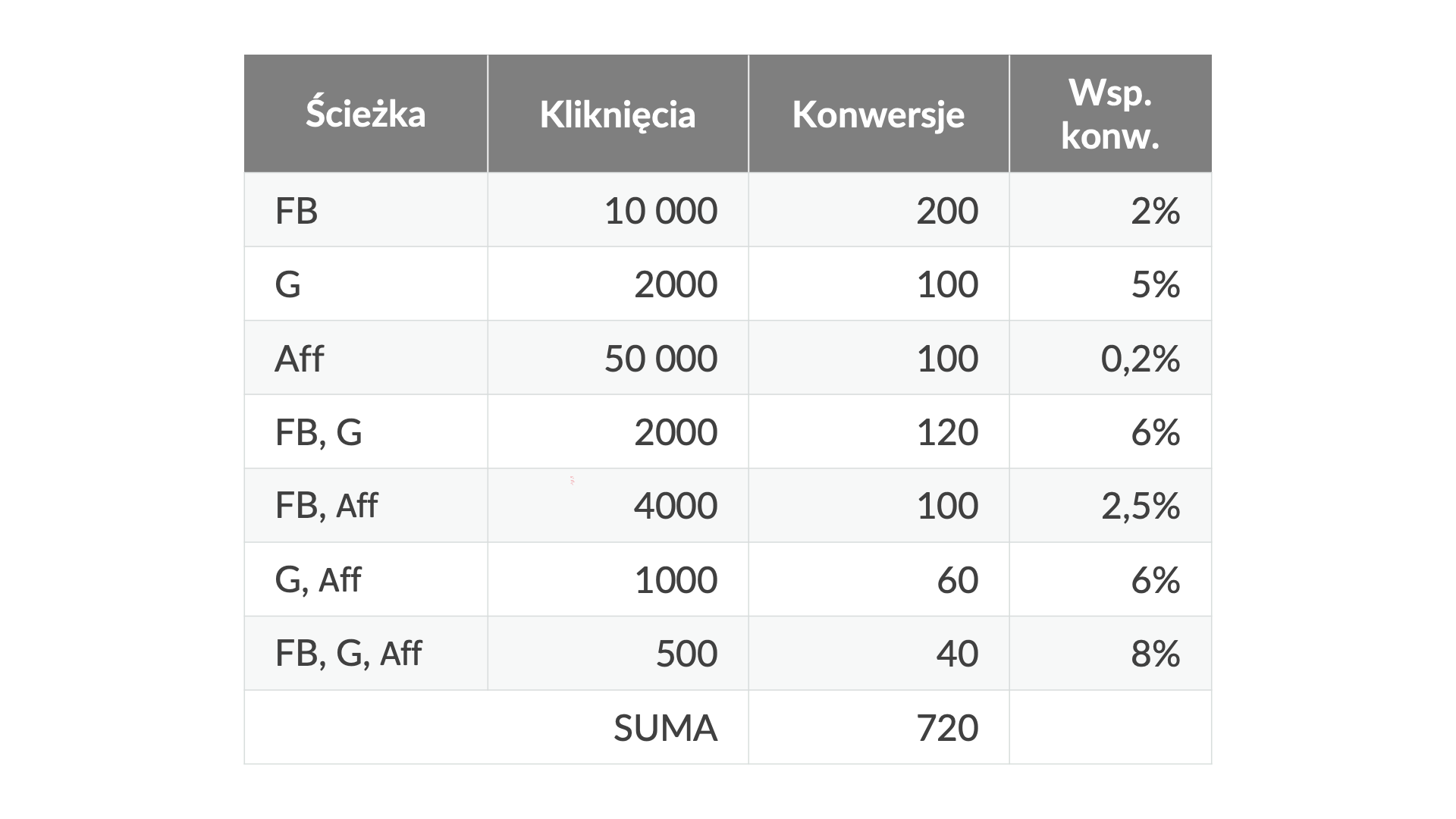
Na początek obliczmy wartość Shapleya dla Facebooka. W tym celu identyfikujemy kombinacje ścieżek zawierające Facebook (FB). Następnie określamy wkład marginalny Facebooka dla każdej z tych ścieżek: od współczynnika konwersji danej ścieżki odejmujemy współczynnik konwersji tejże ścieżki pozbawionej Facebooka.

Przykładowo, dla ścieżki FB, G, której współczynnik konwersji wynosi 6%, ścieżka pozbawiona FB to ścieżka zawierająca tylko G, której współczynnik konwersji wynosi 5%, stąd wkład marginalny Facebooka wynosi 6% – 5% = 1%. Następnie dokonujemy obliczeń zgodnie z formułą wartości Shapleya:

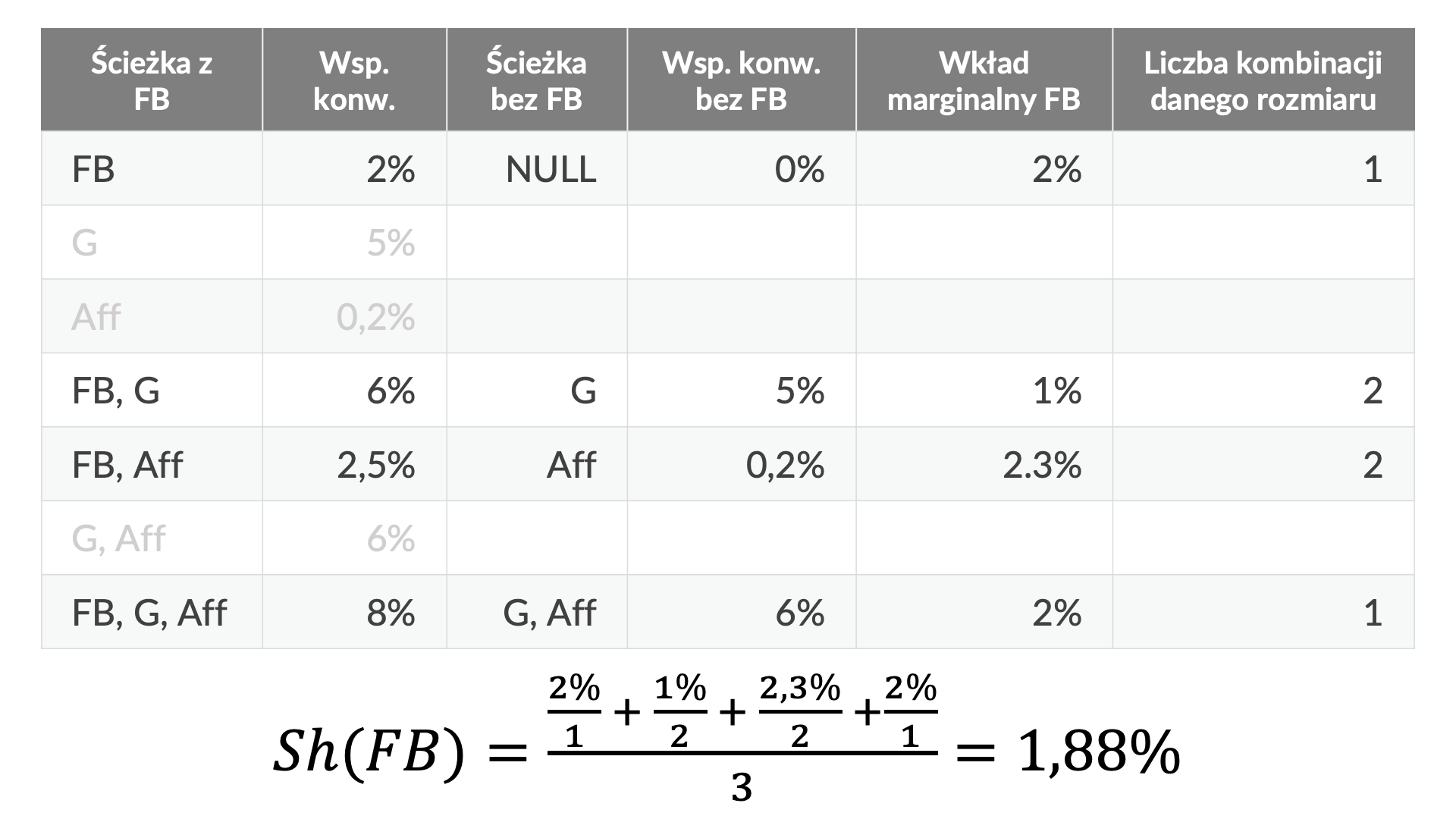
Analogiczne obliczenia wykonujemy dla Google’a (G):

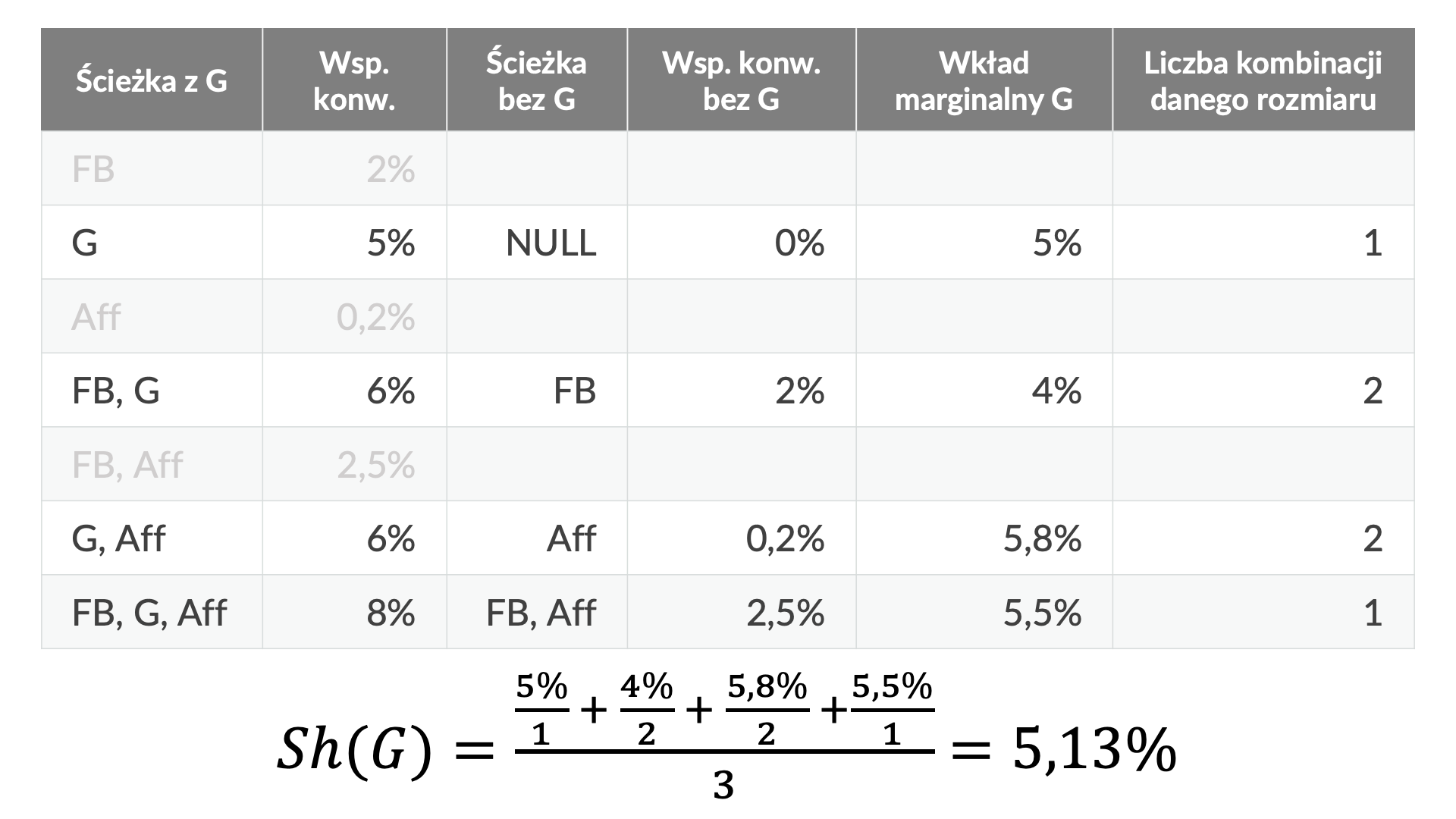
Ponieważ wiemy, że łączny współczynnik konwersji dla wszystkich trzech kanałów wynosi 8%, nie musimy już obliczać formuły wartości Shapleya dla afiliacji. Po prostu odejmiemy udziały Facebooka i Google’a od łącznego wyniku:

Sh(Aff) = 8% – Sh(FB) – Sh(FG) = 8% – 1,88% – 5,13% = 0,98%

Mamy więc już wyliczone wartości Shapleya dla tych źródeł w sytuacji, gdy na ścieżce występują trzy kanały. Dla ścieżek, na których występuje tylko jeden kanał, rozwiązanie jest trywialne – ich udział jest równy współczynnikowi konwersji danej ścieżki:

Teraz musimy dokonać takich samych obliczeń dla kombinacji dwóch kanałów. Obliczmy na początek wartość Shapleya dla Facebooka w kombinacji Facebook + Google:

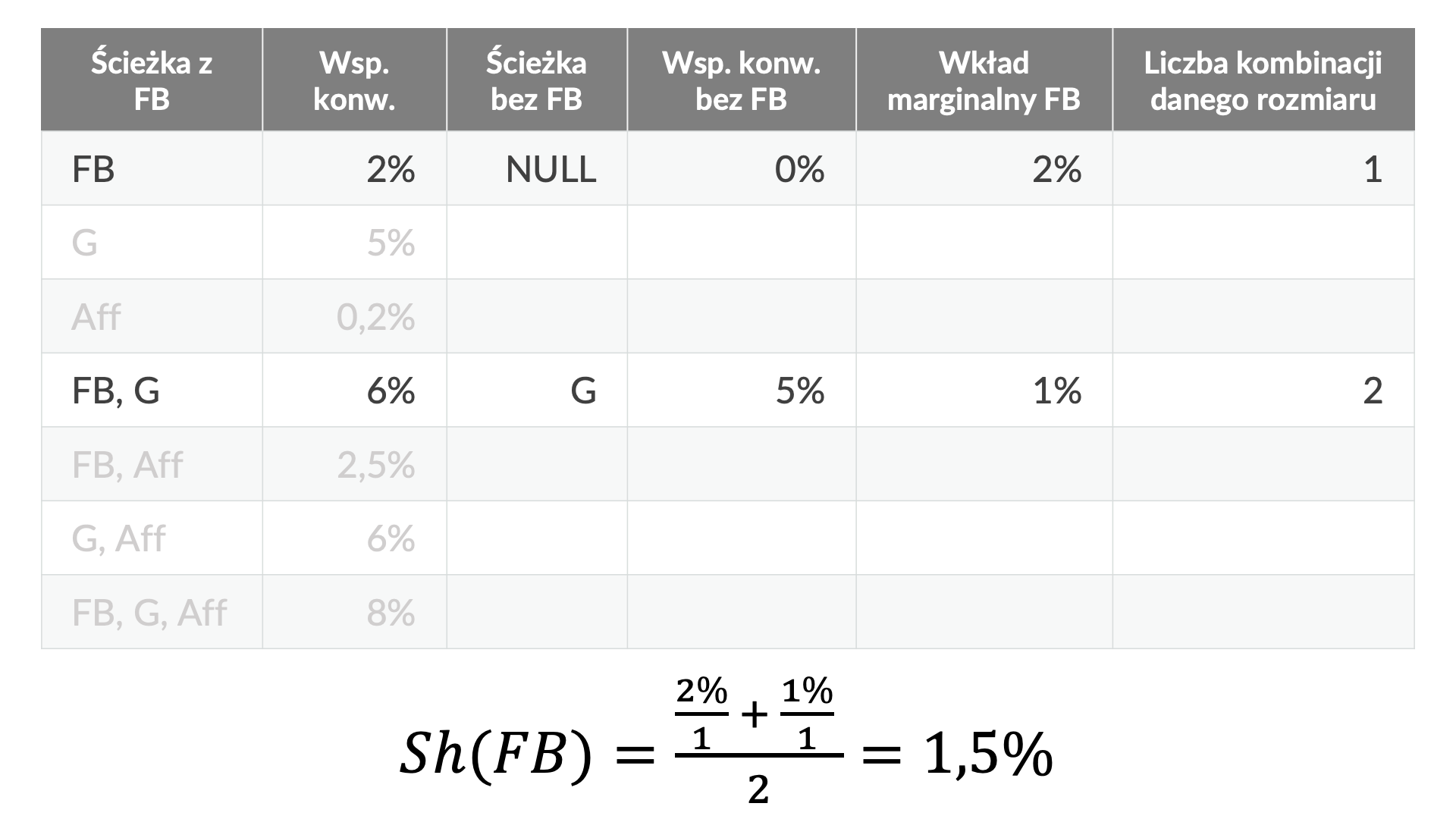
Udział Google będzie różnicą współczynnika konwersji kombinacji Facebook + Google (6%) i wartości Shapleya dla Facebooka (1,5%):

Sh(G) = 6% – Sh(FB) = 6% – 1,5% = 4,5%

Analogiczne obliczenia pozwolą określić wartości Shapleya dla pozostałych kombinacji, a następnie obliczyć konwersje, które przypiszemy do poszczególnych kanałów (liczba konwersji = liczba kliknięć × współczynnik konwersji):

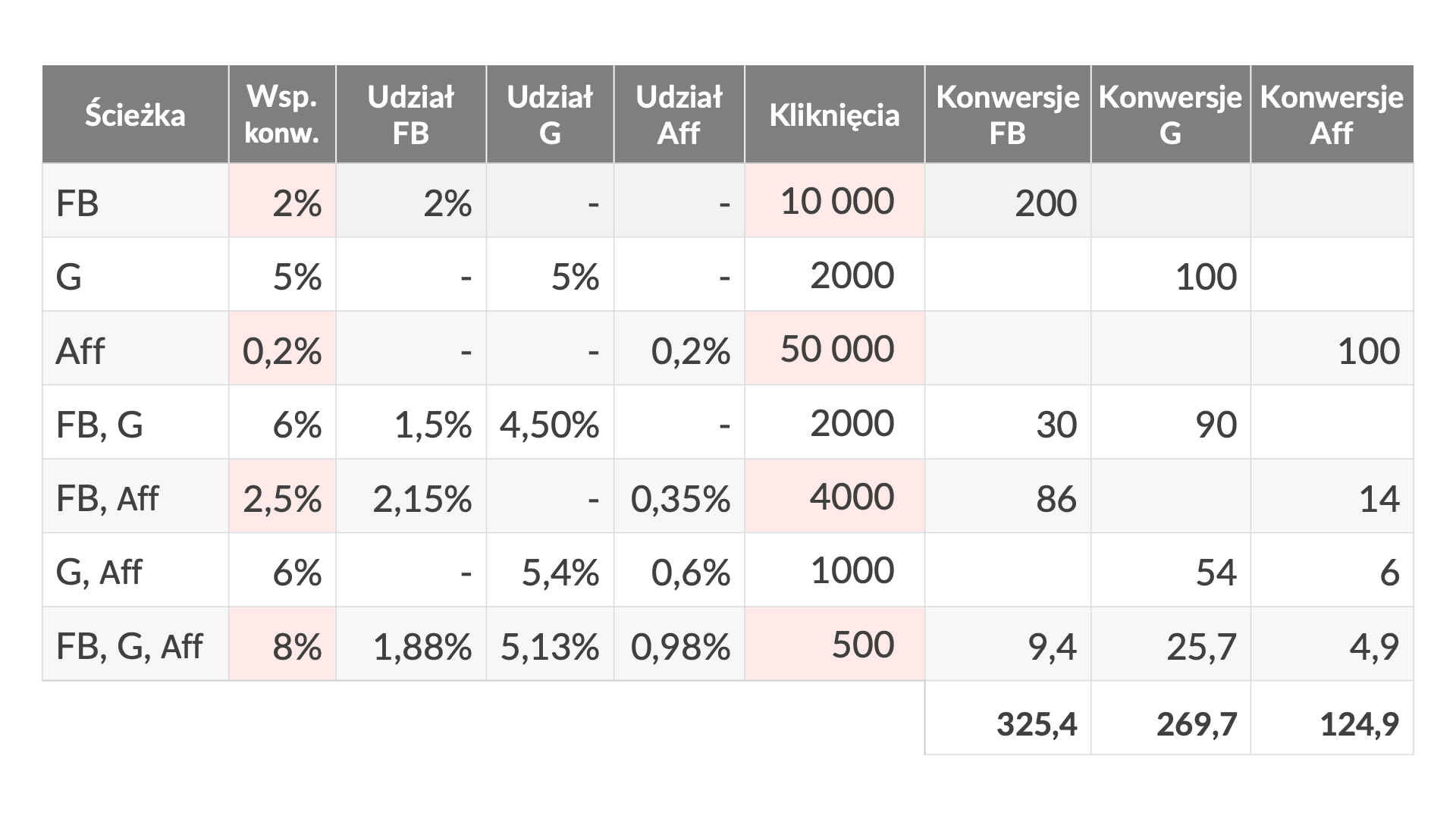
Oczywiście, wartość konwersji przypisanych do poszczególnych źródeł w każdym modelu atrybucji musi się sumować do łącznej liczby wszystkich konwersji (w tym przypadku 325,4 + 269,7 +124,9 = 720).

Wartość Shapleya dla liczby konwersji

Wyliczanie wartości Shapleya dla współczynnika konwersji jest, jak widać, stosunkowo skomplikowane. Dodatkową trudnością jest to, że do jej wyliczenia musimy znać współczynniki konwersji na poszczególnych ścieżkach, a danych tych nie uzyskamy bezpośrednio z Google Analytics, gdyż dostępne są wyłącznie informacje o ścieżkach konwertujących.

Konieczne jest wykorzystanie zaawansowanych segmentów, by na ich podstawie uzyskać dane o liczbie ścieżek, które nie doprowadziły do konwersji, co umożliwi wyliczanie współczynników konwersji danej ścieżki.

A co, gdyby uznać, że wynikiem gry będzie po prostu liczba konwersji? Dane na temat liczby konwersji na poszczególnych ścieżkach dostępne są wprost w raporcie „Najważniejsze ścieżki konwersji” Google Analytics.

Raport ten będzie wymagał pewnych przekształceń, gdyż dla wartości Shapleya nie ma znaczenia kolejność interakcji na ścieżkach. Ścieżki Facebook –> Google oraz Google –> Facebook czy Google –> Facebook –> Google –> Facebook –> Google to po prostu kombinacja Facebook + Google i dane dla nich musimy zagregować.

Kolejnym krokiem będzie obliczenie konwersji skumulowanych, gdyż np. liczba konwersji generowanych przez kombinację Facebook + Google zawiera w sobie również konwersje, które Facebook i Google generują samodzielnie. W przeciwnym wypadku mielibyśmy do czynienia z ujemnymi wkładami marginalnymi.

Podczas dalszych obliczeń wiele operacji się upraszcza i ostatecznie okazuje się, że wartość Shapleya dla konwersji bardzo przypomina model liniowy – konwersje rozdzielane są równo pomiędzy wszystkie kanały występujące na ścieżce (zob. artykuł bit.ly/WartoscShapleya):

Dla ścieżek z naszego przykładu obliczenie tak rozumianej wartości Shapleya dla Facebooka będzie wyglądać następująco:

Ze względu na trywialność tego rozwiązania, wartość Shapleya oblicza się raczej w oparciu o współczynniki konwersji.

Zalety i wady wartości Shapleya

Wartość Shapleya jest pewnego rodzaju uśrednieniem wkładów, które dany kanał wnosi do wyniku uzyskiwanego w każdej z kombinacji kanałów i wydaje się logicznie rozwiązywać podstawowy problem atrybucji, czyli sprawiedliwe uznanie udziału poszczególnych kanałów w konwersji.

Wartość Shapleya bardzo dobrze wykrywa click spam jako kanał, który nic nie wnosi do współczynnika konwersji żadnej ze ścieżek, skutkiem czego zostanie mu przypisana zerowa wartość.

Wartość Shapleya jest koncepcją spójną matematycznie i prawidłowo interpretuje ścieżki jednokanałowe (problem ten występuje w przypadku atrybucji opartej o łańcuchy Markowa – zob. artykuł bit.ly/LancuchyMarkowa).

Google deklaruje, że model atrybucji data-driven w Google Ads i Analytics wykorzystuje wartość Shapleya w swoim algorytmie.

Niestety, ma ona też ograniczenia. Jednym z najczęściej podnoszonych zarzutów jest to, że ignoruje kolejność interakcji. Przykładowo, ścieżki Google –> Facebook i Facebook –> Google są łączone w jedną kombinację Google + Facebook. Tak więc już na samym początku obróbki danych zamazujemy informacje, które intuicyjnie wydają się istotne z punktu widzenia analizy. Ponadto, złożoność obliczeniowa wartości Shapleya rośnie wykładniczo (2ⁿ) wraz z liczbą kanałów biorących udział w procesie konwersji, co znacznie utrudnia jej obliczanie dla większej granulacji kanałów.

W obliczeniach wartości Shapleya brane są po uwagę przede wszystkim współczynniki konwersji, dlatego miara ta premiuje kanały o wyższych współczynnikach konwersji i mocno zaniża te, które samodzielnie nie generują konwersji (takie jak np. remarketing).

Wartość Shapleya jest bardzo wrażliwa na przypadkowe wartości o niewielkiej istotności statystycznej, które traktuje na równi z wiarygodnymi danymi. W połączeniu z faktem, że obliczenia dużej liczby kanałów będą bardzo zasobochłonne, możemy stwierdzić, że wartość Shapleya najlepiej obliczać dla interakcji pogrupowanych w niewielką liczbę kanałów, z których każdy zawiera dane o odpowiedniej istotności statystycznej.

Na koniec warto zauważyć, że wartość Shapleya jest zasilana danymi o wkładach marginalnych wyliczanych na podstawie obserwowanych współczynników konwersji na ścieżkach. Nie jest to pomiar empiryczny.

Jest to jeden z powodów, dla których wartość Shapleya nie interpretuje prawidłowo wkładów wnoszonych przez interakcje, takie jak kliknięcia wyników wyszukiwania słów kluczowych związanych z własną marką. Interakcje te często wiążą się z intencją zakupową, a co za tym idzie – wysokim współczynnikiem konwersji, co interpretowane jest jako wysoki wkład w konwersję, mimo że faktycznie tym interakcjom nie powinna być przypisywana większa wartość.

Podsumowując, wartość Shapleya jest interesującym narzędziem analitycznym wspierającym modelowanie atrybucji, ale z całą pewnością nie jest panaceum na wszystkie problemy związane z właściwą oceną wartości kanałów na wielokanałowych ścieżkach konwersji.

Chcesz dowiedzieć się więcej o modelowaniu atrybucji? Zastanawiasz się, jak możesz zwiększyć zyski ze swoich kampanii? Zapisz się na szkolenia Witolda Wrodarczyka z optymalizowania konwersji i modelowania atrybucji!