Nie wiesz, który model atrybucji zastosować? A co, gdyby to dane mogły dokonać wyboru za Ciebie i określić znaczenie każdej z interakcji na ścieżce konwersji? Próbą rozwiązania tego problemu są zyskujące ostatnio na popularności algorytmiczne modele atrybucji oparte o łańcuchy Markowa.
Od dawna wiadomo, że do transakcji online nie dochodzi zazwyczaj po jednej interakcji; przeważnie jest to konsekwencja wielu wyświetleń, obejrzeń i kliknięć w reklamy, a także konsumpcji innych treści marketingowych. Narzędzia analityczne pozwalają na śledzenie tych ścieżek i modelowanie atrybucji, czyli przypisywanie udziału w konwersjach poszczególnym interakcjom.
Wybór modelu atrybucji
Jednym z największych dylematów, z jakimi się obecnie mierzymy, jest wybór modelu atrybucji. Model liniowy? Rozkład czasowy? A może własny model niestandardowy? Szukając odpowiedzi na to pytanie, najprawdopodobniej znajdziesz wskazówki typu: „Zastanów się, które interakcje są dla Ciebie ważniejsze i przypisz im wyższą wagę” lub „Testuj różne modele i wybierz ten, który się najlepiej sprawdza”. Przyznasz, że nie jest to zbyt pomocne.
Jakakolwiek sztywna reguła zawsze będzie pewnym uproszczeniem, bo każda interakcja może u danego użytkownika odegrać inną, mniej lub bardziej znaczącą rolę. W jednym przypadku kluczowe będzie ostatnie kliknięcie, w innym – ważniejsze będą interakcje wcześniejsze. Tak naprawdę należałoby każdą ze ścieżek przeanalizować indywidualnie.
W tym celu zaczęto tworzyć algorytmiczne modele atrybucji, zwane też modelami opartymi na danych (data-driven attribution). Na podstawie analizy ścieżek konwersji, próbują one określić znaczenie każdej z interakcji i przypisać im odpowiednią wagę, stosownie do roli odegranej na ścieżce. W ostatnim czasie coraz większą popularność zyskują modele algorytmiczne wykorzystujące łańcuchy Markowa.
Czym są łańcuchy Markowa?
Łańcuchy Markowa to proces losowy, w którym prawdopodobieństwo każdego zdarzenia zależy jedynie od zdarzenia poprzedniego.
Przykładem łańcucha Markowa może być następujący proces:
Wyjeżdżam na tygodniowy urlop. To, czy podczas tego urlopu będę uprawiać kontuzjogenny sport, czy oddawać się relaksowi, zależy od tego, gdzie będę spędzać wakacje. Ryzyko wypadku podczas relaksu jest znikome, natomiast sport wiąże się w 1/10 prawdopodobieństwem wypadku:
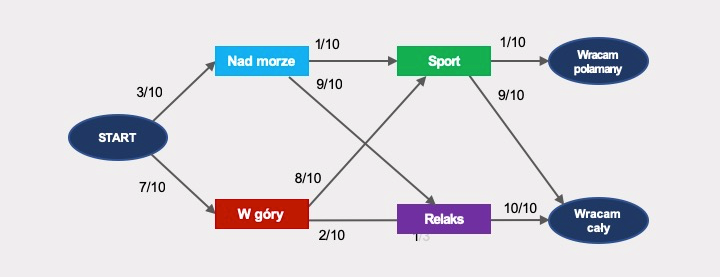
Prawdopodobieństwo, że w dane wakacje wyjadę w góry i ulegnę tam wypadkowi, czyli przejścia START > W góry > Sport > Wracam połamany, wynosi:
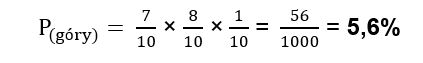
Z kolei szansa, że w wakacje wyjadę nad morze i ulegnę tam wypadkowi, czyli przejścia START > Nad morze > Sport > Wracam połamany, wynosi:
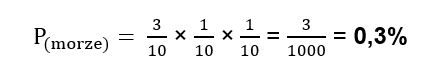
Innej możliwości dojścia do wypadku nie ma. Łączne prawdopodobieństwo wypadku wynosi więc:
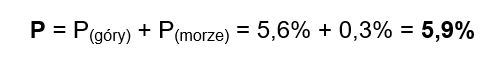
Łańcuch ścieżek konwersji
Załóżmy, że mamy cztery ścieżki interakcji użytkownika z reklamą, z których dwie doprowadziły do konwersji:
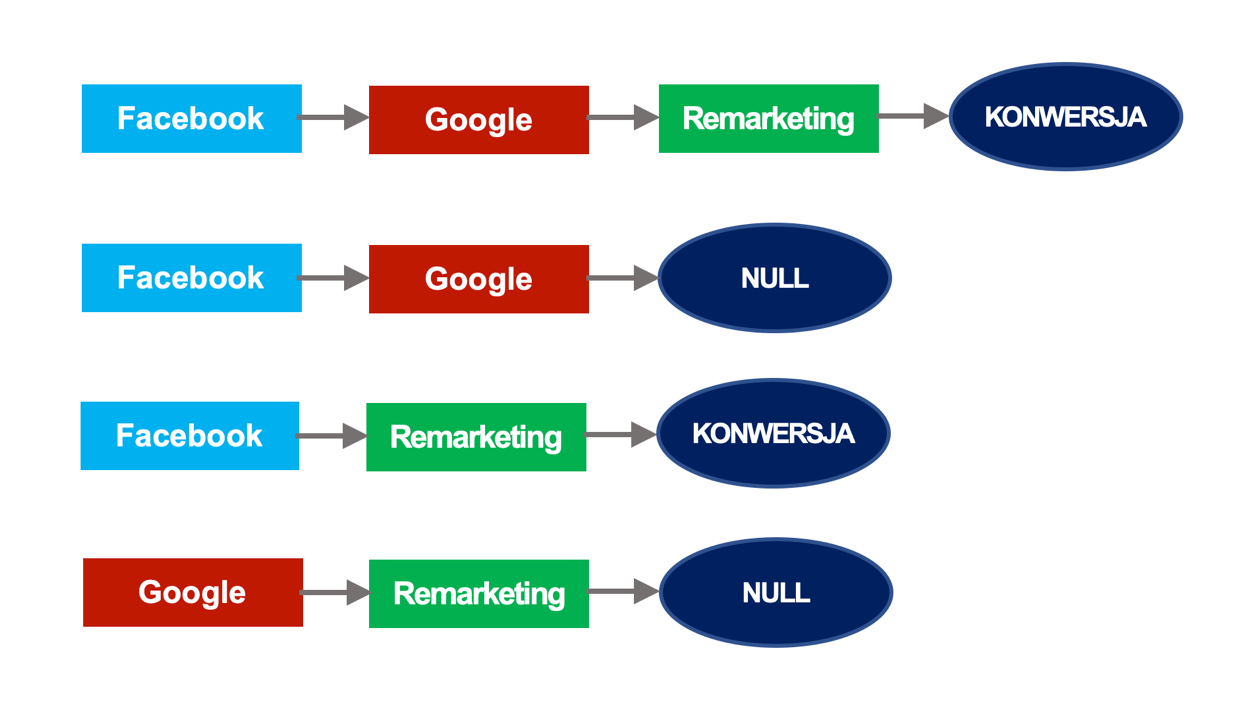
Ścieżki te można przedstawić w postaci grafu, w którym węzłami są poszczególne kanały, połączone łukami w postaci strzałek (zob. rysunek poniżej). Ułamek przy łukach wynika z liczby występujących przejść między węzłami grafu. Interpretujemy go jako prawdopodobieństwo przejścia po danym łuku.
Przykładowo, po interakcji z Facebookiem na dwóch ścieżkach nastąpi interakcja z Google, a na jednej – z remarketingiem. Łącznie są to trzy ścieżki, stąd prawdopodobieństwo tych przejść wynosi odpowiednio 2/3 i 1/3:
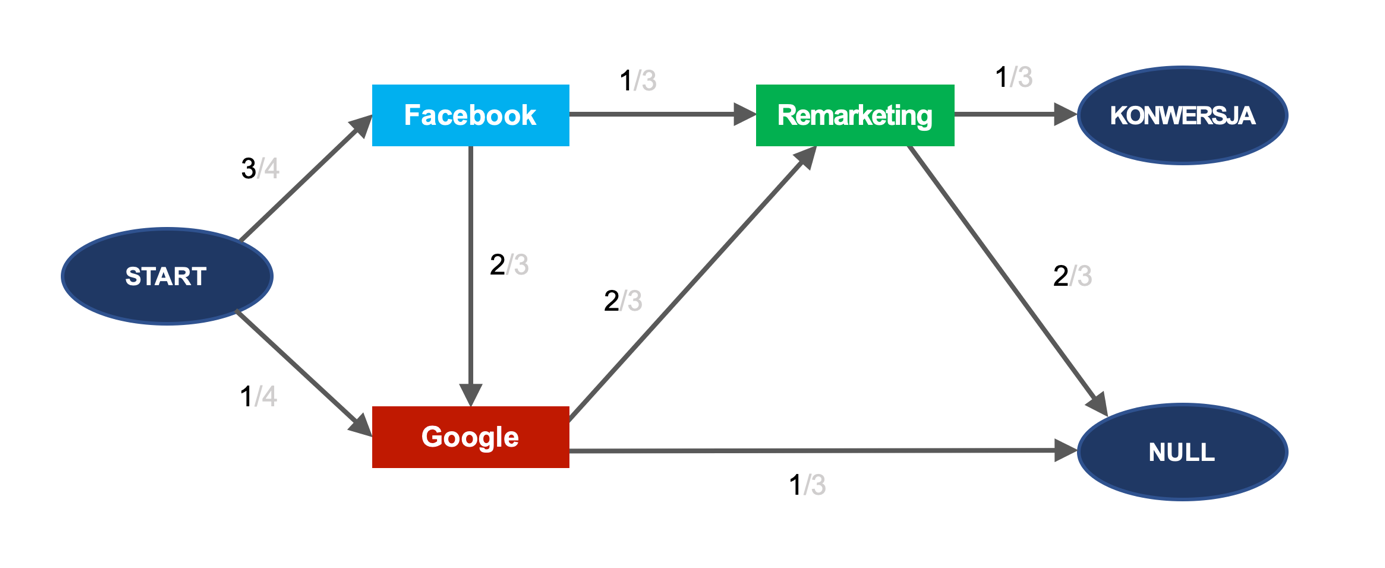
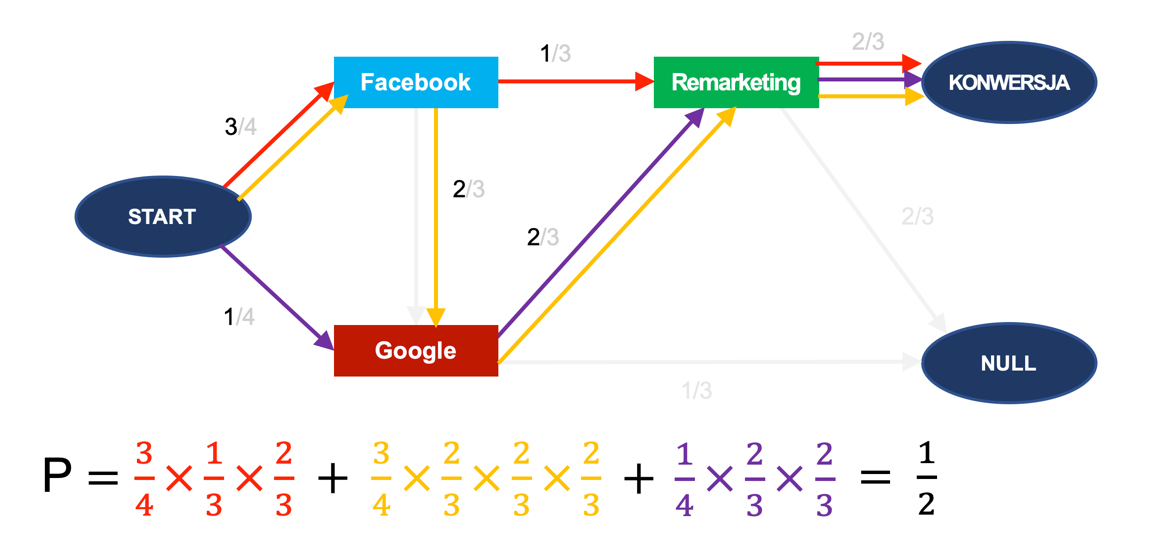
Łączne prawdopodobieństwo konwersji wynosi 1/2 (są tu cztery ścieżki, z których dwie konwertują). Prawdopodobieństwo to można też obliczyć, sumując prawdopodobieństwo przejść po wszystkich możliwych ścieżkach w grafie, które prowadzą od węzła START do węzła KONWERSJA:
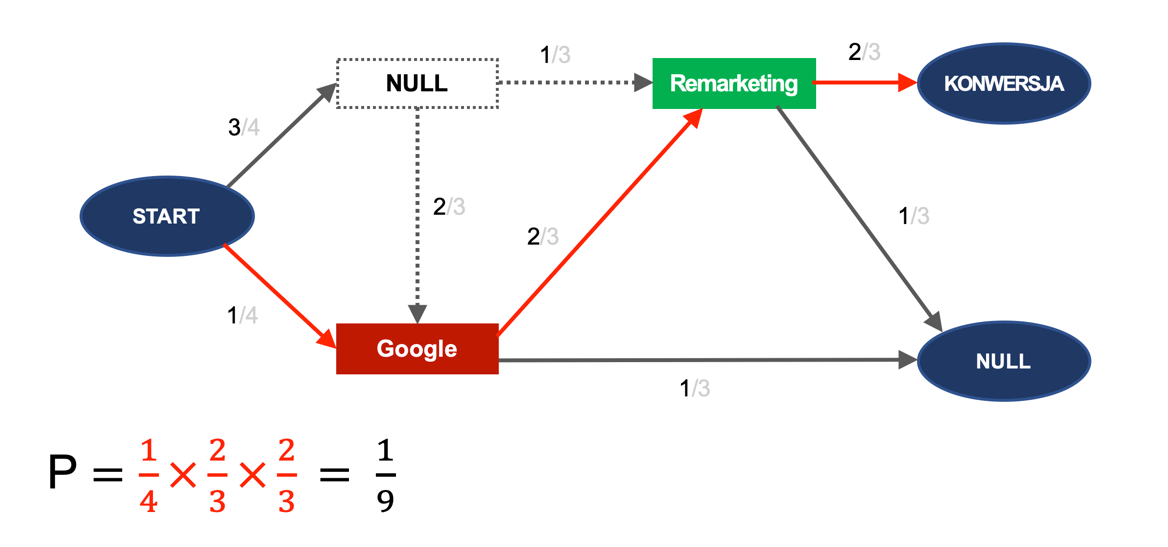
Zobacz teraz, jak zmieni się prawdopodobieństwo konwersji w przypadku usunięcia jednego z kanałów. Po usunięciu Facebooka jest tylko jedna ścieżka prowadząca do konwersji z prawdopodobieństwem 1/9:
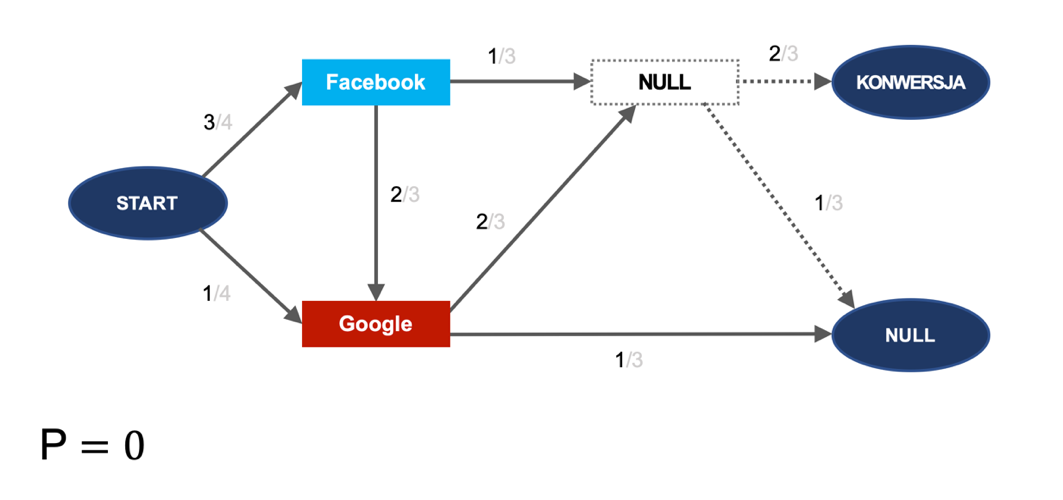
Analogicznie, po usunięciu Google’a, prawdopodobieństwo konwersji wynosi 1/6:
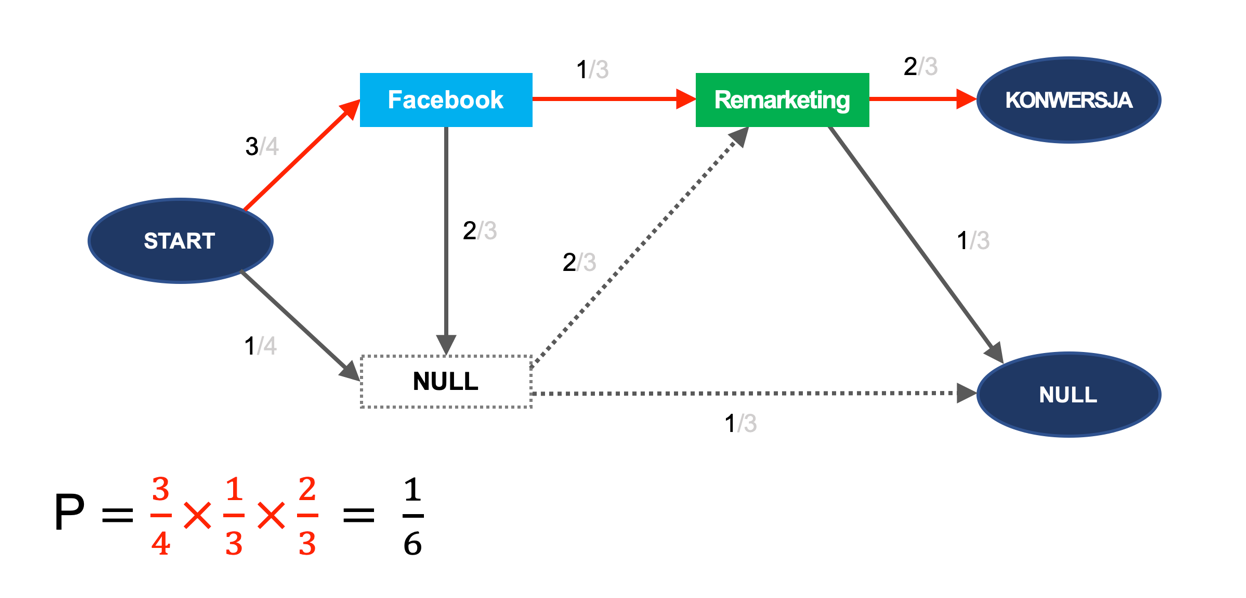
Z kolei usunięcie remarketingu powoduje, że po grafie nie można dotrzeć do konwersji, czyli jej prawdopodobieństwo wynosi 0:
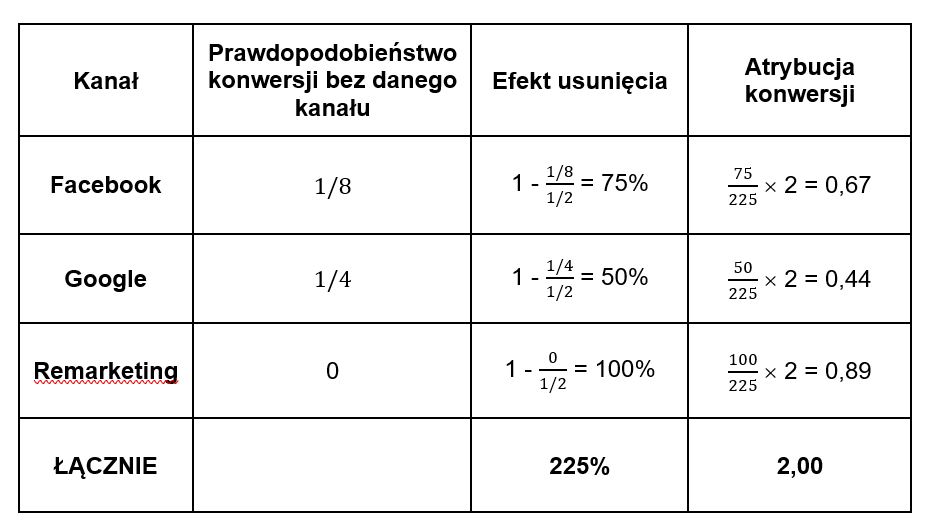
Teraz trzeba obliczyć tzw. efekt usunięcia. Określa on spadek prawdopodobieństwa konwersji na skutek usunięcia poszczególnych kanałów. Przykładowo, po usunięciu Google’a, prawdopodobieństwo konwersji spada z 1/2 do 1/6, czyli o 66,7% (zob. tabela poniżej).
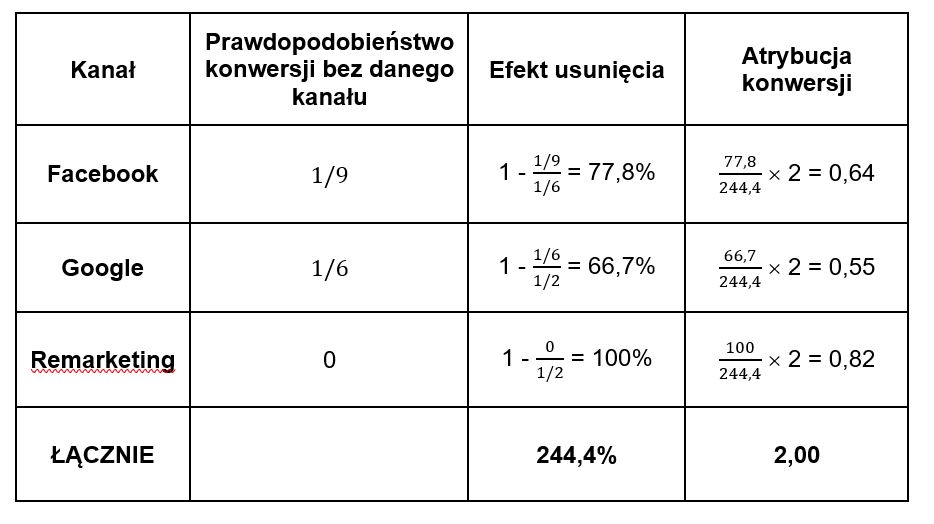
Widzimy, że efekty usunięcia nie sumują się do 100%. Z tego powodu, aby obliczyć udział w wyniku dla poszczególnych kanałów, obniżamy je proporcjonalnie, tak by sumowały się do jedności.
Na koniec, aby obliczyć atrybucję konwersji, mnożymy łączną liczbę konwersji (w tym przykładzie są to dwie konwersje) przez udział w wyniku.
Brak ścieżek niekonwertujących
Raport ścieżek konwersji Google Analytics zawiera jedynie ścieżki prowadzące do konwersji:
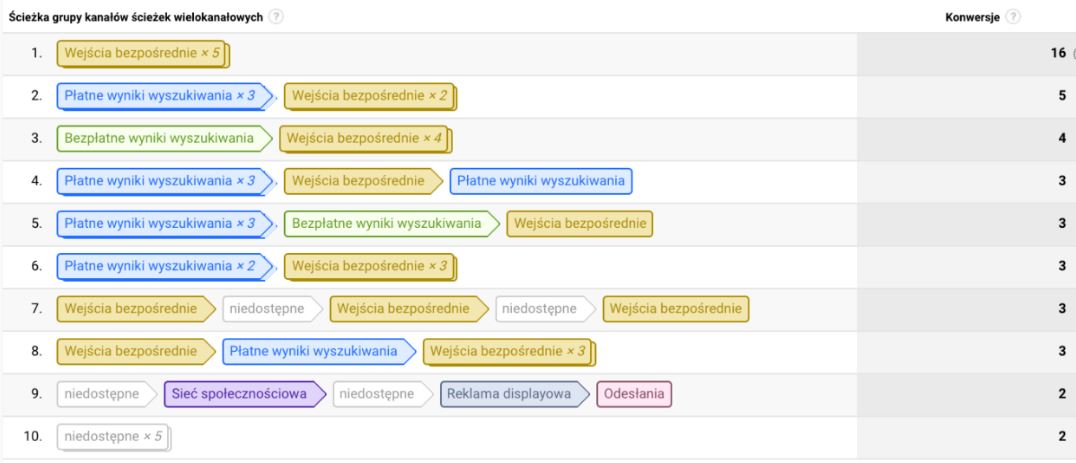
Raporty dotyczące ścieżek niekonwertujących nie są bezpośrednio dostępne. Na szczęście, łańcuchy Markowa można również tworzyć dla danych zawierających wyłącznie ścieżki konwertujące. Ścieżki konwertujące w omawianym wcześniej przykładzie wyglądają następująco:
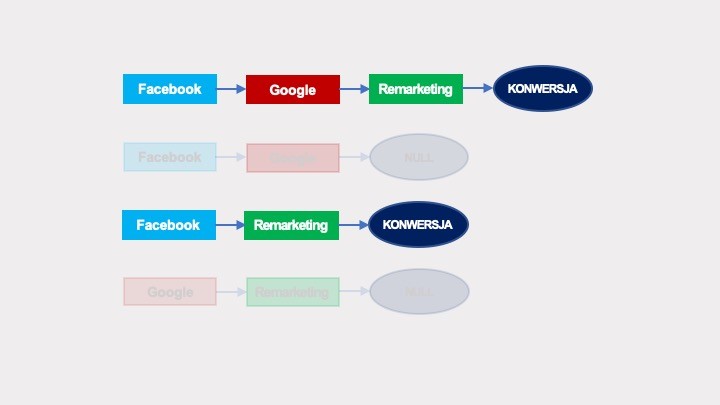
Po przekształceniu w graf:
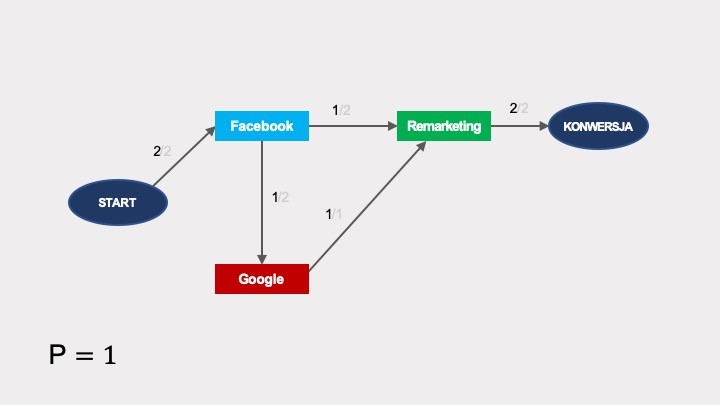
W takim łańcuchu prawdopodobieństwo konwersji wynosi 1, ponieważ wszystkie ścieżki do niej prowadzą.
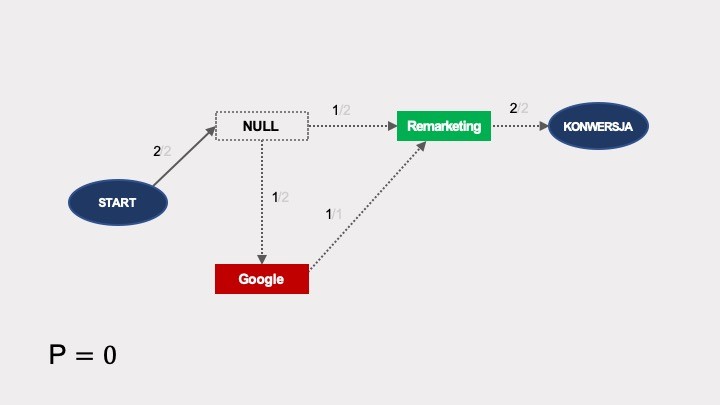
Podobnie jak w poprzednich przykładach, trzeba teraz obliczyć efekt usunięcia dla poszczególnych kanałów. Prawdopodobieństwo konwersji po usunięciu Facebooka jest zerowe:
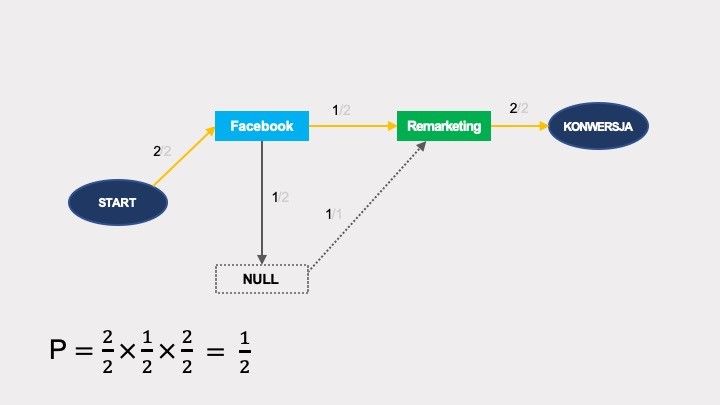
Po usunięciu Google’a prawdopodobieństwo konwersji wynosi 1/2:
Po usunięciu remarketingu prawdopodobieństwo konwersji wynosi 0:
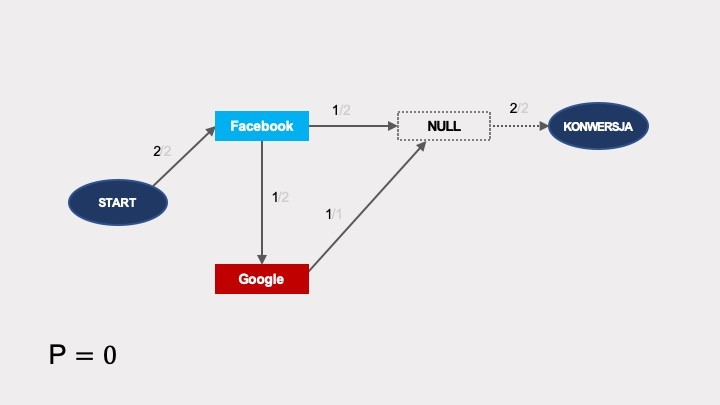
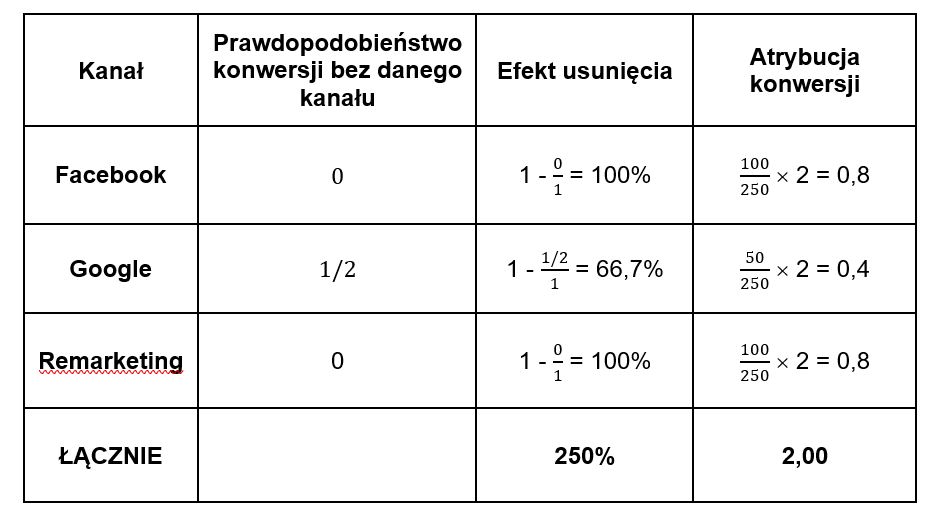
W ten sposób można obliczyć efekty usunięcia i udział w konwersjach dla poszczególnych kanałów:
Łańcuchy Markowa wyższego rzędu
Zgodnie z definicją, w łańcuchach Markowa prawdopodobieństwo każdego zdarzenia zależy jedynie od zdarzenia poprzedniego. Mówi się, że węzły klasycznego łańcucha Markowa „nie mają pamięci”.
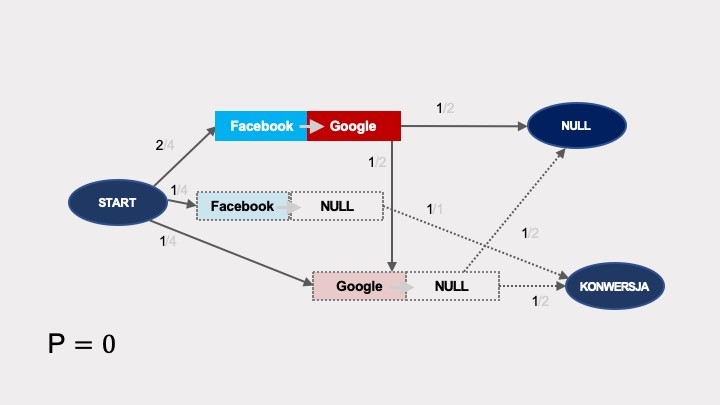
Co to oznacza w praktyce? Spójrz na poniższy graf. Prawdopodobieństwo konwersji po interakcji z remarketingiem wynosi 2/3, niezależnie od tego, czy wcześniejsza wizyta była z Facebooka, czy z Google’a:
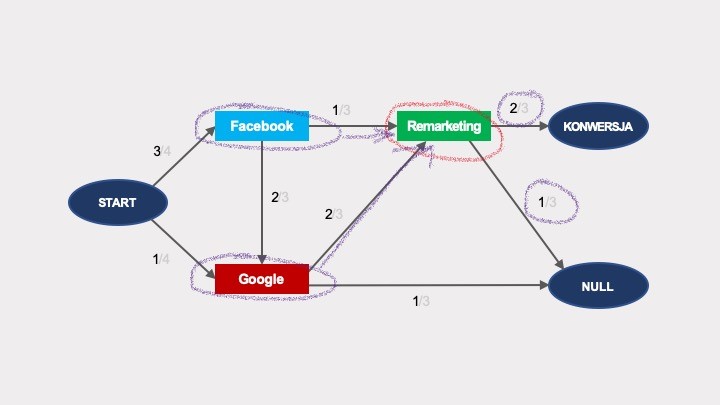
Wiemy, że w rzeczywistości nie jest to prawda. Skuteczność remarketingu będzie diametralnie inna w zależności od tego, skąd przyszedł dany użytkownik, czy będzie to osoba, która wcześniej szukała Twojego produktu w Google, czy ktoś, kogo zaciekawił Twój post na Facebooku. Tę kwestię rozwiązują łańcuchy Markowa wyższego rzędu. W przypadku łańcuchów drugiego rzędu, prawdopodobieństwo przejścia do kolejnych węzłów zależy również od stanu poprzedniego. Zamiast pojedynczych interakcji, należy analizować ich pary:
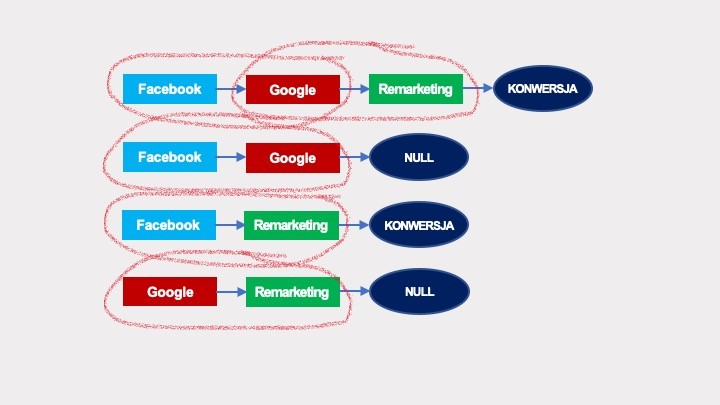
Graf łańcuchów Markowa będzie wyglądał w tym przypadku następująco:
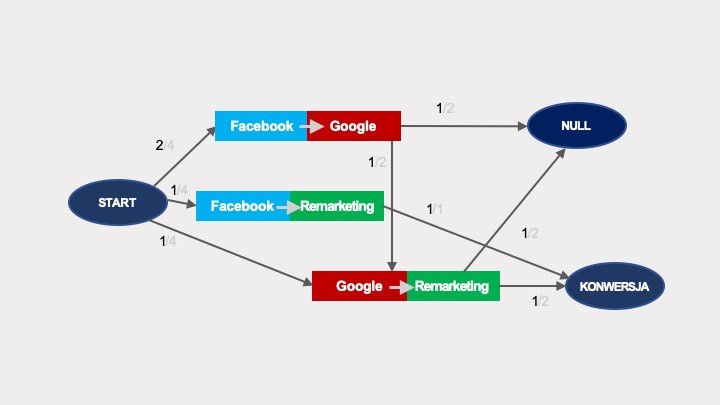
Obliczenia prawdopodobieństwa wykonywane są w analogiczny sposób jak w przypadku łańcuchów Markowa pierwszego rzędu. Prawdopodobieństwo przejścia do konwersji (możliwe na trzy sposoby, zaznaczone kolorami) wyliczane na podstawie tego grafu wynosi niezmiennie 1/2:
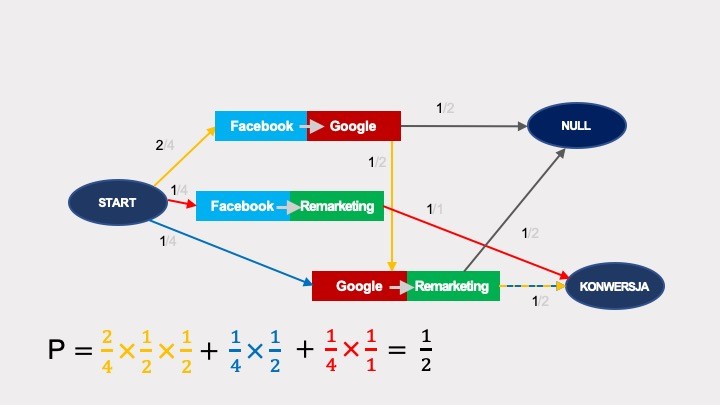
Podobnie jak we wcześniejszych przykładach oblicza się efekty usunięcia. Usunięcie Facebooka spowoduje zniknięcie wszystkich węzłów par interakcji zawierających Facebooka:
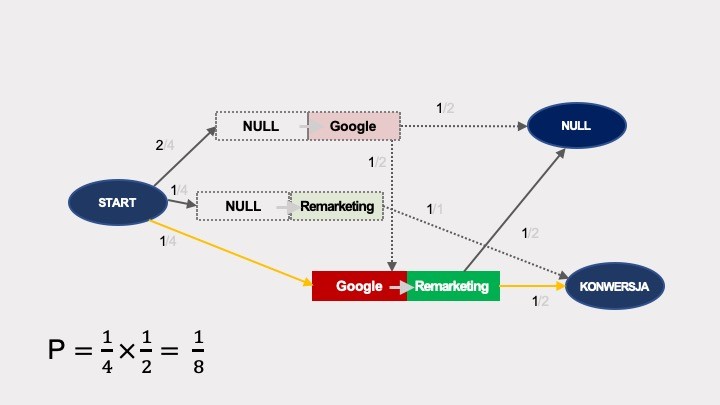
Analogicznie wyliczany jest efekt usunięcia Google’a:
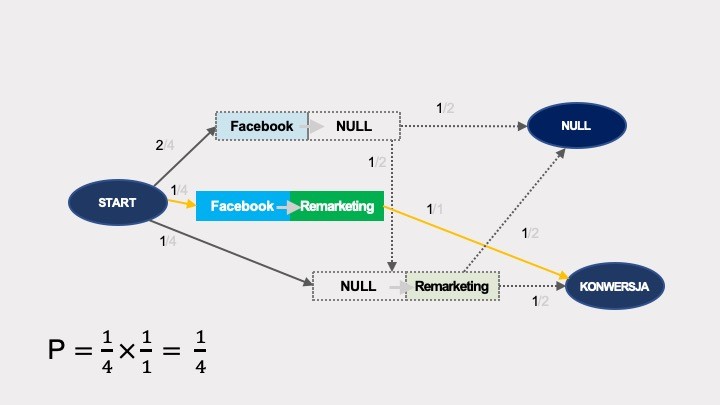
…oraz remarketingu:
Obliczenia efektów usunięcia i udziałów w wyniku są identyczne jak we wcześniejszych przykładach:
Można tworzyć też łańcuchy Markowa trzeciego, czwartego i dalszych rzędów. Ich węzły będą miały jeszcze dłuższą „pamięć”, a prawdopodobieństwo przejścia do kolejnych węzłów będzie zależało od dwóch, trzech, itd. poprzednich stanów. W praktyce rzadko używa się łańcuchów rzędu wyższego niż czwarty.
Jeśli chcesz poznać więcej aspektów związanych z modelowaniem atrybucji z wykorzystaniem łańcuchów Markowa, przeczytaj artykuł na blogu Adequate.
Czy to już model idealny?
Łańcuchy Markowa są interesującym modelem algorytmicznym, pozwalającym uwzględniać sekwencję interakcji. Nie są jednak pozbawione wad.
Przy modelowaniu z wykorzystaniem łańcuchów Markowa będziesz często obserwować, że kanały, które występują jako jedyne na ścieżce (ścieżki jednokanałowe), mogą tracić udział w konwersjach na rzecz innych kanałów. A przecież to nie ma sensu! Jeśli na ścieżce jest tylko jedna interakcja, całość konwersji powinna być przypisana właśnie jej.
Sposobem na poprawienie tego mankamentu jest wydzielenie ścieżek jednokanałowych i analiza wyłącznie tych ścieżek, które zawierają dwie lub więcej interakcji. Nie zmienia to faktu, że model oparty na łańcuchach Markowa obarczony jest pewnym błędem, widocznym nawet w trywialnym przypadku ścieżek jednokanałowych.
Mimo że model ten wciąż jest pewnym przybliżeniem, analiza atrybucji z wykorzystaniem łańcuchów Markowa – w porównaniu z liniowym i innymi modelami – może dostarczyć wartościowych sygnałów do analizy.
PORADA
Na stronie: bit.ly/MarkovTool znajdziesz bezpłatne narzędzie, które umożliwia samodzielne wyliczenie atrybucji opartej o łańcuchy Markowa z następującymi opcjami:
- uwzględnienie ścieżek konwertujących i niekonwertujących lub tylko konwertujących,
- łańcuchy Markowa pierwszego, drugiego, trzeciego i czwartego rzędu,
- możliwość oddzielnego wyliczenia ścieżek jednokanałowych.
Dostępne obecnie algorytmiczne modele atrybucji nie wydają się być jeszcze rozwiązaniami ostatecznymi. Ich ograniczenia wynikają nie tylko z samych modeli matematycznych. Znacznie ważniejszym problemem jest kompletność danych. Oparte na plikach cookie pomiary konwersji nie są odpowiednie do śledzenia użytkowników korzystających z różnych urządzeń i przeglądarek. Występują też ograniczenia w raportowaniu wyświetleń reklamy, a niektóre media po prostu nie poddają się śledzeniu dostępnymi metodami (np. działania w niektórych aplikacjach czy reklama offline).
Coraz więcej użytkowników korzysta też z trybu incognito, a same przeglądarki wprowadzają ograniczenia w zbieraniu informacji (np. Intelligent Tracking Prevention w Safari czy planowane zmiany w Chrome), co może bardzo ograniczyć śledzenie użytkownika przy pomocy obecnych technologii.
Nawet najdoskonalszy model, działający na niekompletnych danych, będzie wyciągał błędne wnioski. Techniki uzupełniania brakujących danych opierają się w dużej mierze na próbkowaniu i ekstrapolacji, co stanowi dodatkowe utrudnienie.
Z całą pewnością, daleko jeszcze do uzyskania idealnego narzędzia, które będzie automatycznie wspierać decyzję o przydziale budżetu na poszczególne kanały marketingowe. Do tego czasu algorytmiczne modele atrybucji będą ważnym, ale wciąż jedynie wspomagającym narzędziem w złożonym procesie optymalizacji stawek i alokacji budżetów.

 7 min
7 min 

 Poznań
Poznań







Przypominamy, że wielkimi krokami zbliża się konferencja I ♥ Marketing & Technology, która odbędzie się już 22–24 października 2024 roku oraz organizowane przez nas 33 szkolenia z zakresu marketingu.
Jeśli chcesz być zawsze na bieżąco, zamów prenumeratę magazynu sprawny.marketing!